Matrix puzzle

I recently saw a problem from an Indian maths olympiad:

There is a square arrangement made out of n elements on each side (n^2 elements total). You can put assign a value of +1 or -1 to any element. A function f is defined as the sum of the products of the elements of each row, over all rows and g is defined as the sum of the product of elements of each column, over all columns. Prove that, for n being an odd number, f(x)+g(x) can never be 0.

There is a very quick solution, similar in flavour to that famous dominoes puzzle. However, I didn’t come up with it immediately, and my investigation led down an interesting route.

Preliminary observations

It is easy to see that given a matrix of \(1\) and \(-1\), we have \(f, g\) unchanged on reordering rows and columns, and on taking the transpose. This leads to a very useful lemma: \(f, g\) are unchanged if we negate the corners of a rectangle in the matrix.

The idea then occurs: perhaps there is a normal form of some kind?

Specification of normal form

Given any four -1’s laid out at the corners of a rectangle, we may flip them all into 1’s without changing \(f, g\). Similarly, given any three -1’s on the corners of a rectangle, where the fourth corner is 1, we may flip to get a rectangle with one -1 and three 1’s.

Repeat this procedure until there are no rectangles with three or more corners -1. (Note that we might get a different answer depending on the order we do this in!) A Mathematica procedure to do this (expressed in a very disgusting way) is as follows. {% raw %} internalReduce[mat_] := Module[{m = mat}, Do[If[(i != k && j != l) && Count[Extract[m, {{i, j}, {k, j}, {i, l}, {k, l}}], -1] > 2, {m[[i, j]], m[[i, l]], m[[k, j]], m[[k, l]]} = -{m[[i, j]], m[[i, l]], m[[k, j]], m[[k, l]]}; ], {i, 1, Length[mat]}, {j, 1, Length[mat]}, {k, 1, Length[mat]}, {l, 1, Length[mat]}]; m] reduce[mat_] := FixedPoint[internalReduce, mat] {% endraw %}

Notice that columns which contain more than one -1 must not overlap, in the sense that no two columns with more than one -1 may have a -1 in the same row. Indeed, if they did, we’d have a submatrix somewhere of the form {{-1, -1}, {1, -1}}, which contradicts the “we’ve finished flipping” condition. Hence we may rearrange rows so that all -1’s appear together in contiguous columns.

We may then rearrange columns so that reading from the left, we see successive columns with decreasingly many -1’s. Rearrange rows again so that they appear stacked on top of each other.

example of reduced matrix

We’ve ended up with a normal form: columns of -1’s, diagonally adjoined to each other, followed by rows of -1’s. (The following Mathematica code relies on the fact that SortBy is a stable sort.)

normalform[mat_] := SortBy[Transpose@SortBy[Transpose@reduce[mat], -Count[#, -1] &], Count[#, -1] /. {0 -> Infinity} &]

We haven’t shown that it’s unique yet, and indeed it’s not. As a counterexample, {{-1,1,1,1,1}, {-1,1,1,1,1}, {1,-1,1,1,1}, {1,-1,1,1,1}, {1,1,1,1,1}} is transformed into {{-1,1,1,1,1}, {-1,1,1,1,1}, {-1,1,1,1,1}, {-1,1,1,1,1},{1,1,1,1,1}} by a rectangle-flip.

This suggests a further improvement to the normal form: by flipping in this way, we may insist that any column of -1’s, other than the first, must contain only one -1. Indeed, if it contained two or more, we would flip two of them into the first column, rearrange so that all columns were contiguous -1’s again, and repeat.

What does our matrix look like now? It’s a column of -1, followed by some diagonal -1’s, followed by a row of -1. We’ll call this the canonical form, although I’ve still not shown uniqueness.

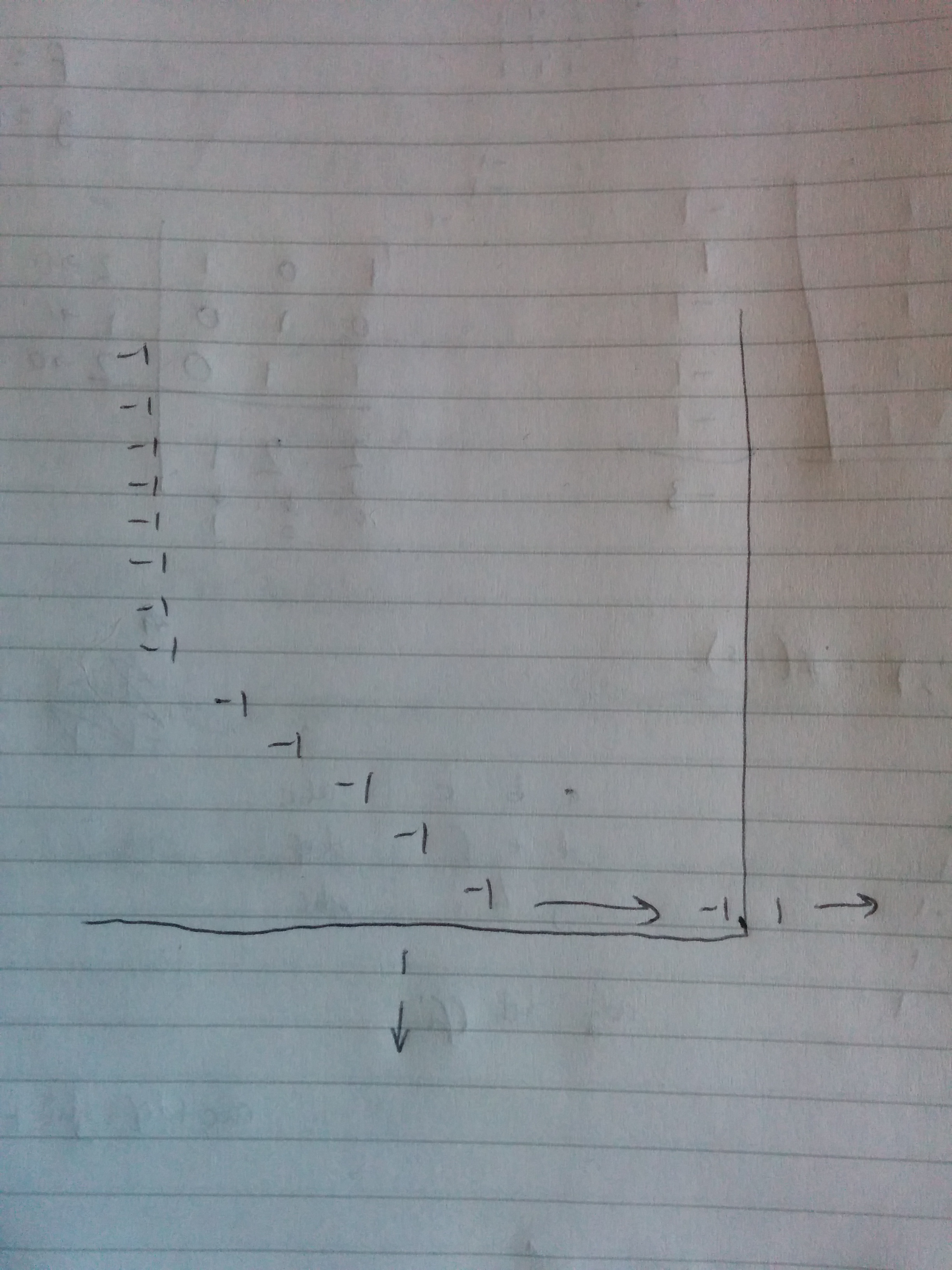
example of matrix in canonical form

Restatement of problem

The problem then becomes: given a matrix in canonical form, show that \(f+g\) cannot be 0.

Notice that if the long column is \(r\) long, and there are \(s\) diagonal -1’s, and the long row is \(t\) long, and the matrix is \(n \times n\), then \(f = -r-s+(-1)^t + (n-s-r-1)\), \(g = -t-s+(-1)^r + (n-s-t-1)\).

Hence \(f+g = 2n - 2(r+2s+t+1) + (-1)^r + (-1)^t\).

Any choice of \(r, s, t, n\) with \(r+s+1 \leq n; s+t+1 \leq n; r, t>1\) yields a valid matrix. We therefore need to show that for all \(r, s, t, n\) we have \(2(n-r-2s-t-1) + (-1)^r + (-1)^t \not = 0\).

Solution

Reducing this mod 4, it is enough to show that \(2(n-r-t-1) + (-1)^r + (-1)^t \not \equiv 0 \pmod{4}\). But we can easily case-bash the four cases which arise depending on the odd-even parity of \(r, t\), to see that in all four cases, the congruence does indeed not hold.

\(r, t\) even: \(2(n-1) + 2 = 2n\), but since \(n\) is odd, this is not \(0 \pmod{4}\).
\(r\) even, \(t\) odd: \(2n - 1\), since \(t-1\) is even so \(2(t-1)\) is a multiple of 4. \(2n-1\) isn’t even even, let alone divisible by \(4\).
\(r, t\) odd: \(2(n-1) + 2 = 2n\) which is again not \(0 \pmod{4}\).

Summary